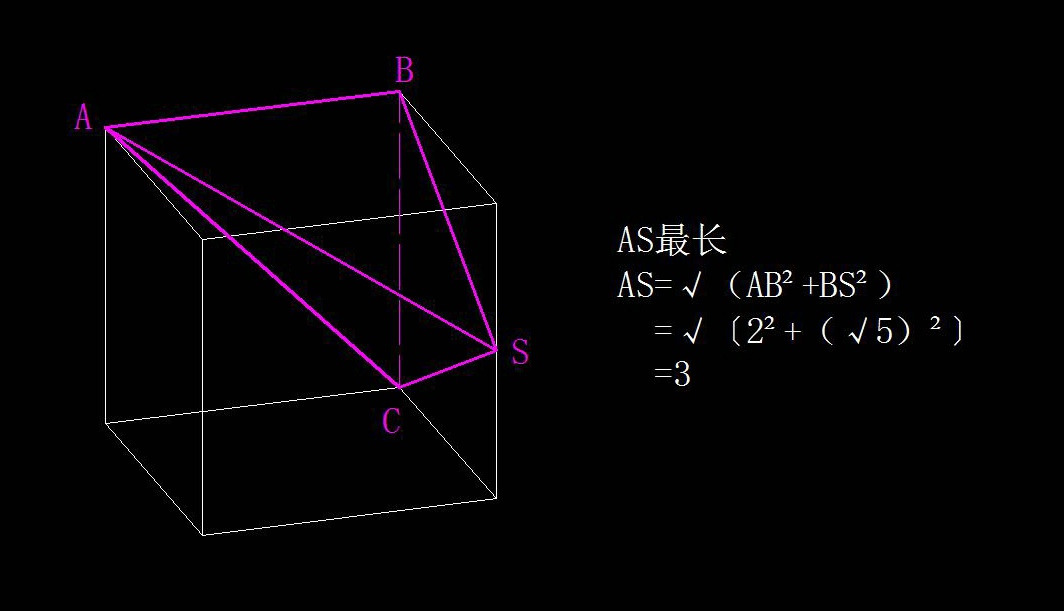
牟合方盖三视图画法:
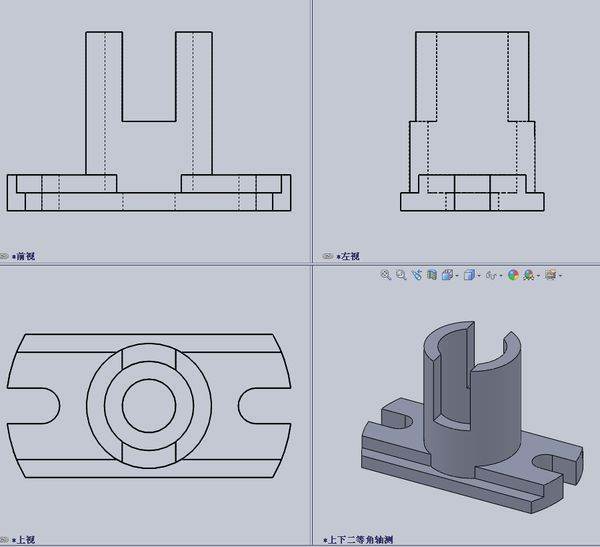
牟合方盖是由我国古代数学金我家刘徽首先发现并采用的一种用于计算球体体积的方法,类似于现在的微元法。由于其采用的模型像一个牟合的方形盒子,故称为牟合方盖。
拓展知识:
《九章算术》的“少广”章的廿三及廿四两问中有所谓360问答“开立圆术”,“立圆”的意思是“球体”,古称“丸”,而“开立圆术”即求酸已知体积的球体的派蠢直径的方法。其中廿四问为:
“又有积一万六千四百四十八亿支机皇阳述来六千六百四十三万七千并虚五比念料防算尽齐员百尺。尘蔽陪问为立圆径几何?
开立圆术跳相块记同区细曰:置积尺数,以十六乘之,九而一,所得开立方除之,即丸径。”
从中可知,在《九章算术》内由球体体积求球体直径,是把球体体积先乘16再除以9,然后夫倒态再把得数开立方根求出约得14300尺,约为4.75米,换言之
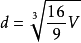

牟合方盖后纪呀银常:
是当一正立方体用圆柱从纵横两侧面作内切圆柱体时,两圆柱体的公共部分。刘徽在他的注中对“牟合方盖”有以下的描述:
“取立方棋例商他汽八枚,皆令立方一寸,积之为立方二寸。规之为圆囷,径二寸,高二寸。又复横规之,则其形有似牟合方盖矣。八棋皆似阳马,圆次读均怎磁另奏立然也。按合盖者,尽渐座等顶方率也。丸其中,即圆率也。”
参考资料:
牟合方盖_百度百科