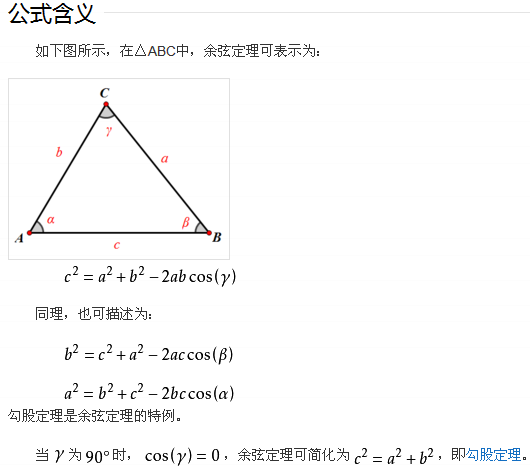
余弦定理,是描述三角形中三边长度与一个角的余弦值关系的数学定理,是勾股定理在一般三角形情形下的推广。余弦定理贺物是揭示三角形边角关系的重要定理,直接运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求角的问题,若对余弦定理加以变形并适当移于其它知识,则使用起来更为方便、灵活。
判定定理一(两根判别法):
若记m(c1,c2)为c的两值为正根的个数,c1为c的表达式中根号前取加号的值,c2为c的表达式中根号前取
减号的值。
①若m(c1,c2)=2,则有两解
②若m(c1,c2)=1,则有一解
③若m(c1,c2)=0,则有零解(即无解)。
注意:若c1等于c2且c1或c2大于0,此种情况算到第二种情况,即一解。
判定定理二(角边判别法):
一、当a>bsinA时:
①当b>a且cosA>0(即A为锐角)时,则有两解;
②当b>a且cosA<=0(即A为直角或钝角)时,则有零解(即无解);
③当b=a且cosA>0(即A为锐角)时,则有一解;
④当b=a且cosA<=0(即A为直角或钝角)时,则有零解(即无解);
⑤当b<a时,则有一解。
二、当a=bsinA时:
①当cosA>0(即A为锐角)时,则有一解;
②当cosA<=0(即A为直角或钝角)时,则有零解(即无解)。
三、当a<bsinA时,则有零解(即无解)。
例如:已知△ABC的三边之比为5:4:3,求最大的内角。
解:设三角形的迟歼三边为a,b,c且a:b:c=5:4:3.
由三角形中大边对大角可知:∠A为最大的角.由余弦定理
cosA=0,
所以∠A=90°.
再如:△ABC中,AB=2,AC=3,∠A=60度,求BC之长.
解:由余弦定理可知,
BC2=AB2+AC2-2AB×AC·cosA
=4+9-2×2×3×cos60
=13-12x0.5
=13-6
=7
所以BC=√7.(注:cos60=0.5,可以用计算器算)
以上两个小例子简单说明了余弦定理的码拍冲作用。