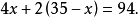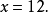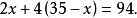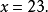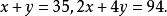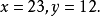理解
中国古代《孙子算经》共三卷,成书大约在公元5世纪。这本书浅显易懂,有许多有趣的算术题,比如“鸡兔同笼”问题:
今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?
题正物嫌目中给出雉兔共有35只,如果把兔子的两只前脚用绳子捆起来,看作是一只脚,两只后脚也用绳子捆起来,看作是一只脚,那么,兔子就成了2只脚,即把兔子都先当作两只脚的 鸡。鸡兔总的脚数是35×2=70(只),比题中所说的94只要少94-70=24(只)。
松开一只兔子脚上的绳子,总的脚数就会增加2只,即70+2=72(只),再松开一只兔子脚上的绳子,总的脚数又增加2,2,2,2……,一直继续下去,直至增加24,因此兔子数:24÷2=12(只),从而鸡有35-12=23(只)。
我们来总结一下这道题的解题思路:如果先假设它们全是鸡,于是根据鸡兔的总数就可以算出在假设下共有几只脚,把这样得到的脚数与题中给出的脚数相比较,看看差多少,每差2只脚就说明有1只兔,将所差的脚数除以2,就可以算出共有多少只兔。概括起来,解鸡兔同笼题的基本关系式是:兔数=(实际脚数-每只鸡脚数×鸡兔总数)÷(每只兔子脚数-每只鸡脚数)。类似地,也可以假设全是兔子。
思路
"鸡兔同笼"是一类有名的中国古算题。最早出现在《孙子算经》中.许多小学算术应用题都可以转化成这类问题,或者用解它的典型解法--"假设法"来求解。因此很有必要学会它的解法和思路.
例1 有若干只鸡和兔子,它们共有88个头,244只脚,鸡和兔各有多少只
解:我们设想,每只鸡都是"金鸡独立",一只脚站着;而每只兔子都用两条后腿,像人一样用两只脚站着,地面上出现脚的总数的一半,·也就是
244÷2=122(只)
在122这个数里,鸡的头数算了一次,兔子的头数相当于算了两次。因此从122减去总头数88,剩下的就是兔子头数
122-88=34(只),
有34只兔子,当然鸡就有54只。
答:有兔子34只,鸡54只。
上面的计算,可以归结为下面算式:
总脚数÷2-总头数=兔子数. 总头数-兔子数=鸡数
上面的解法是《孙子算经》中记载的。做一次除法和一次减法,马上能求出兔子数,多简单!能够这样算,主要利用了兔和鸡的脚数分别是4和2,4又是2的2倍.可是,当其他问题转化成这类问题时,"脚数"就不一定是4和2,上面的计算方法就行不通。因此,我们对这类问题给出一种一般解法.
还说例1.
如果设想88只都是兔子,那么就有4×88只脚,比244只脚多了
88×4-244=108(只).
每只鸡比兔子少(4-2)只脚,所以共有鸡
(88×4-244)÷(4-2)= 54(只).
说明我们设想的88只"兔子"中,有54只不是兔子。而是鸡.因此可以列出公式
鸡数=(兔脚数×总头数-总脚数)÷(兔脚数-鸡脚数).
当然,我们也可以设想88只都是"鸡",那么共有脚2×88=176(只),比244只脚少了
244-176=68(只).
每只鸡比每只兔子少(4-2)只脚,
68÷2=34(只).
说明设想中的"鸡",有34只是兔子,也可以列出公式
兔数=(总脚数-鸡脚数×总头数)÷(兔脚数-鸡脚数).
上面两个公式不必都用,用其中一个算出兔数或鸡数,再用总头数去减,就知道另一个数。
假设全是鸡,或者全是兔,通常用这样的思路求蚂笑解,有人称为"假设法".
拿一个具体问题来试举手试上面的公式。
例2 红铅笔每支0.19元,蓝铅笔每支0.11元,两种铅笔共买了16支,花了2.80元。问红,蓝铅笔各买几支?
解:以"分"作为钱的单位.我们设想,一种"鸡"有11只脚,一种"兔子"有19只脚,它们共有16个头,280只脚。
现在已经把买铅笔问题,转化成"鸡兔同笼"问题了.利用上面算兔数公式,就有
蓝笔数=(19×16-280)÷(19-11)
=24÷8
=3(支).
红笔数=16-3=13(支).
答:买了13支红铅笔和3支蓝铅笔。
对于这类问题的计算,常常可以利用已知脚数的特殊性.例2中的"脚数"19与11之和是30.我们也可以设想16只中,8只是"兔子",8只是"鸡",根据这一设想,脚数是
8×(11+19)=240(支)。
比280少40.
40÷(19-11)=5(支)。
就知道设想中的8只"鸡"应少5只,也就是"鸡"(蓝铅笔)数是3.
30×8比19×16或11×16要容易计算些。利用已知数的特殊性,靠心算来完成计算.
实际上,可以任意设想一个方便的兔数或鸡数。例如,设想16只中,"兔数"为10,"鸡数"为6,就有脚数
19×10+11×6=256.
比280少24.
24÷(19-11)=3,
就知道设想6只"鸡",要少3只。
要使设想的数,能给计算带来方便,常常取决于你的心算本领.
例题
例3 一份稿件,甲单独打字需6小时完成.乙单独打字需10小时完成,甲单独打若干小时后,因有事由乙接着打完,共用了7小时。甲打字用了多少小时?
解:我们把这份稿件平均分成30份(30是6和10的最小公倍数),甲每小时打30÷6=5(份),乙每小时打30÷10=3(份).
现在把甲打字的时间看成"兔"头数,乙打字的时间看成"鸡"头数,总头数是7."兔"的脚数是5,"鸡"的脚数是3,总脚数是30,就把问题转化成"鸡兔同笼"问题了。
根据前面的公式
"兔"数=(30-3×7)÷(5-3)
=4.5,
"鸡"数=7-4.5
=2.5
也就是甲打字用了4.5小时,乙打字用了2.5小时。
答:甲打字用了4小时30分.
例4 1998年时,父母年龄(整数)和是78岁,兄弟的年龄和是17岁。四年后(2002年)父的年龄是弟的年龄的4倍,母的年龄是兄的年龄的3倍.那么当父的年龄是兄的年龄的3倍时,是公元哪一年?
解:4年后,两人年龄和都要加8.此时兄弟年龄之和是17+8=25,父母年龄之和是78+8=86。我们可以把兄的年龄看作"鸡"头数,弟的年龄看作"兔"头数。25是"总头数",86是"总脚数"。根据公式,兄的年龄是
(25×4-86)÷(4-3)=14(岁).
1998年,兄年龄是
14-4=10(岁).
父年龄是
(25-14)×4+4=40(岁).
因此,当父的年龄是兄的年龄的3倍时,兄的年龄是
(40-10)÷(3-1)=15(岁).
这是2003年。
答:公元2003年时,父年龄是兄年龄的3倍.
例5蜘蛛有8条腿,蜻蜓有6条腿和2对翅膀,蝉有6条腿和1对翅膀。这三种小虫共18只,有118条腿和20对翅膀.每种小虫各几只?
解:因为蜻蜓和蝉都有6条腿,所以从腿的数目来考虑,可以把小虫分成"8条腿"与"6条腿"两种。利用公式就可以算出8条腿的
蜘蛛数=(118-6×18)÷(8-6)
=5(只).
因此就知道6条腿的小虫共
18-5=13(只).
也就是蜻蜓和蝉共有13只,它们共有20对翅膀。再利用一次公式
蝉数=(13×2-20)÷(2-1)=6(只).
因此蜻蜓数是13-6=7(只).
答:有5只蜘蛛,7只蜻蜓,6只蝉。
例6 某次数学考试考五道题,全班52人参加,共做对181道题,已知每人至少做对1道题,做对1道的有7人,5道全对的有6人,做对2道和3道的人数一样多,那么做对4道的人数有多少人?
解:对2道,3道,4道题的人共有
52-7-6=39(人).
他们共做对
181-1×7-5×6=144(道).
由于对2道和3道题的人数一样多,我们就可以把他们看作是对2.5道题的人((2+3)÷2=2.5).这样
兔脚数=4,鸡脚数=2.5,
总脚数=144,总头数=39.
对4道题的有
(144-2.5×39)÷(4-2.5)=31(人).
答:做对4道题的有31人。
以例1为例 有若干只鸡和兔子,它们共有88个头,244只脚,鸡和兔各有多少只?
以简单的X方程计算的话,我们一般用设大数为X,那么也就是设兔为X,那么鸡的只数就是总数减去鸡的只数,即(88-X)只。
解:设兔为X只。则鸡为(88-X)只。
4X+2×(88-X)=244
上列的方程解释为:兔子的脚数加上鸡的脚数,就是共有的脚数。4X就是兔子的脚数,2×(88-X)就是鸡的脚数。
4X+2×88-2X=244
2X+176=244
2X+176-176=244-176
2X=68
2X÷2=68÷2
X=34
即兔子为34只,总数是88只,则鸡:88-34=54只。
答:兔子有34只,鸡有54只。
公式1:(兔的脚数×总只数-总脚数)÷(兔的脚数-鸡的脚数)=鸡的只数
总只数-鸡的只数=兔的只数
公式2:( 总脚数-鸡的脚数×总只数)÷(兔的脚数-鸡的脚数)=兔的只数
总只数-兔的只数=鸡的只数
公式3:总脚数÷2—总头数=兔的只数
总只数—兔的只数=鸡的只数
公式4:鸡的只数=(4×鸡兔总只数-鸡兔总脚数)÷2 兔的只数=鸡兔总只数-鸡的只数
公式5:兔总只数=(鸡兔总脚数-2×鸡兔总只数)÷2 鸡的只数=鸡兔总只数-兔总只数
公式6 :4×+2(总数-x)=总脚数 (x=兔,总数-x=鸡数,用于方程)
假设法
假设全是鸡:2×35=70(只)
鸡脚比总脚数少:94-70=24 (只)
兔子比鸡多的脚数:4-2=2(只)
兔子的只数:24÷2=12 (只)
鸡的只数:35-12=23(只)
方程法
一元一次方程
解:设兔有x只,则鸡有(35-x)只。
解得
鸡:35-12=23(只)
解:设鸡有x只,则兔有(35-x)只。
解得
兔:35-23=12(只)
答:兔子有12只,鸡有23只。
注:通常设方程时,选择腿的只数多的动物,会在套用到其他类似鸡兔同笼的问题上,好算一些。
二元一次方程组
解:设鸡有x只,兔有y只。
解得
答:兔子有12只,鸡有23只。
抬腿法
方法一
假如让鸡抬起一只脚,兔子抬起2只脚,还有94÷2=47(只)脚。笼子里的兔就比鸡的脚数多1,这时,脚与头的总数之差47-35=12,就是兔子的只数。
方法二
假如鸡与兔子都抬起两只脚,还剩下94-35×2=24只脚 , 这时鸡是屁股坐在地上,地上只有兔子的脚,而且每只兔子有两只脚在地上,所以有24÷2=12只兔子,就有35-12=23只鸡。
方法三
我们可以先让兔子都抬起2只脚,那么就有35×2=70只脚,脚数和原来差94-70=24只脚,这些都是每只兔子抬起2只脚,一共抬起24只脚,用24÷2得到兔子有12只,用35-12得到鸡有23只。