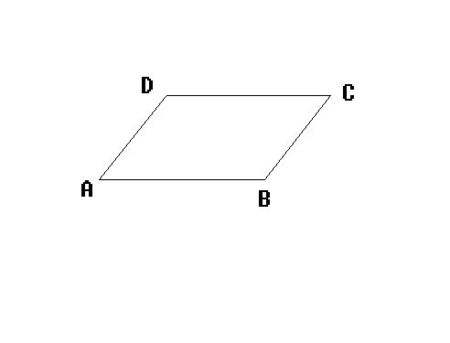
∠B和∠D的度数均为120°。
解答过程:
因为AD平行于BC,所以可得∠A和∠C为对角,∠B和∠D为对角。
∠A的度数为60°,且平行四边形对角的度数相等,橘桐搜因此∠C也为60°
∠A+∠C的度数为120°。
因为平行四边形的内角和为360°,所以∠B+∠D的度数为:360°-120°=240°
因此,∠B和∠D的度数均为:240°÷2=120°。
拓展资料:
平行四边形,是在同一个二维平面内,由两组平行线段组成的闭合图形。平行四边形一般用图形名称加四个顶点依次命名。注:在用字母表示四边形时,一定要按顺时针或逆时针方向注明各顶点。
在欧几里德几何中,平行四边形是具有两对平行边的简单(非自相交)四边形。 平行四边形的相对或相对的侧面具有相同的长度,并且平行四边形的相反的角度是相等的。
平行四边形的性质:
(矩形、菱形、正方形都是特殊的平行四边形。)
(1)如果一个四边形是平行四边形,那么这个四边形的两组对边分别相等。
(简述为“平行四边形的两组对边分别相等”)
(2)如果一个四边形是平行四边形,那么这个四边形的两组对角分别相等。
(简述为“平行四边形的两组对角分别相等” )
(3)如果一圆历个四边形是平行四边形,那么这个四边形的邻角互补。
(简述为“平行四边形的邻角互补”)
(4)夹在两条平行线间的平行的高相等。(简述为“平行线间的高距离处处相等”)
(5)如果一个四边形是平行四边形,那么这个四边形的两条对角线互相平分。
(简述为“平行四边形的对角线互相平分”)
(6)连接任意四边形各边的中点所得图形是平行四边形。(推论)
(7)平行四边形的面积等于底和高的积。(可视为矩形。)
(8)过平行四边形对角线交点的直线,将平行四边形分成全等的两部分图形。
(9)平行四边形是中心对称图形,对称中心是两对角线的交点.
(10)平行四边形不是轴对称图形,但平行四边形是中心对称图形。矩形和菱形是轴对称图形。注:正方形,矩形以及菱形也是一种特殊的平行四边形,三者具有平行四边形的性质。
(11)平行四边形ABCD中(如图)E为AB的中点,则AC和DE互相三等分,一般地,若E为AB上靠近A的n等分点,则AC和DE互相(n+1)等分。
(12)平行四边形ABCD中,AC、BD是平行四边形ABCD的对角线,则各四边的平方和等于对角线的平方和。
(13)平行四边形对角线把平行四边形面积分成四等份。
(14)平行四边形中,两条在不同对边上的高所组成的夹角,较小的角等于平行四边形中较小的角,较大的角等于平行四边形中较大的角。
(15)平行四边形的面积等于相邻两边与其夹角正弦的乘积轮轿。
参考资料:平行四边形-百度百科