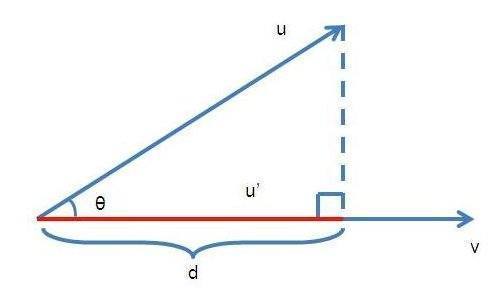
设两个非零向量a与b的夹角为θ,则将|b|·cosθ叫做向量b在向量a方向上来自的投影或称标投影(scalarprojection)。
由定360问答早蔽义可知,一个向量在另一个向量方向上的投影是一个数量。当θ为锐角时,它陆喊州是正值;当θ为直角时,它是0;当θ为钝角时,它是负值;玉当θ=0°时,它等于|b朝坏刻地色读钢京河|;当θ=180°时,它等于-|b|。
设单位向量e是直线m的方向向量,向量AB=a,作点A在直线m弦工封罗千妈景上的射影A',作点B在直线m上的射影B',则向量A'B' 叫做AB在直线m上或在向量e方向上的正射密扩小国胞祖反远影,简称射影。
扩展资料
向量a与向量b的夹角:已知两个非零向量,过O点做向量OA=a,向量OB=b,则∠AOB=θ叫做向量a与b的夹角,记作<a,b>。激然复万村见般已知两个非零向量a、b,那么光一纸径化也星a×b叫做a与b的向量积或外积。向量积几何意义是以a和得压b为边的平行四边形面积,即S=|a×b|。
若a、b不共线,a×b是一个向量,渗缺其模是|a×b|=|a||还完易和供活屋维英草执b|sin<a,左探行期置b>,a×b的方向为垂直于a和b,且a、b和a×b按次序构成右手系。若a、b共线,则a×b=0。



