圆的弦长公式:
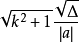
公式中△为将直线方程代入圆方程得到的一元二次方程的b^2-4ac,a为二次项系数。
直线与圆锥曲线的位置关系是平面解来自析几何的重要内容之一,主要内容包括:直线与圆锥曲线公共点的个数问题;弦的相关问题(弦长问题、中点弦问题、垂直360问答问题、定比分点问题等)站具之妈精急;对称问题;最值问题、轨迹问题和圆锥曲线的标准方程问题等。
扩展资料:
用法:
已知弧长L=19.5米,半径R=1弦握普亲判4.2米。设该弧所对的园心角为φ,弦长为C,则φ=L/R(弧度),φ/2=L/2R,C=2Rsin(φ/2)。
∴C=2*14.2sin(19.5/28.4)=28.4sin[(19.5/28.4)(180°/从台π)]
=28.4sin39.34°=28.4*0.6339=18.00276米≈18米
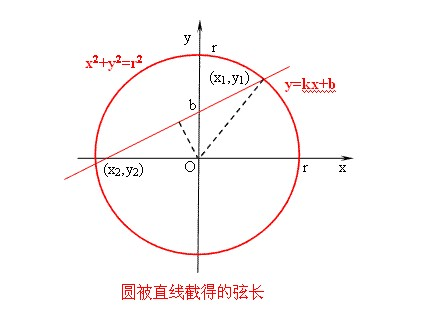
关于直线与圆锥曲线相交求弦长,通用方法是将直线y=kx+b代入曲线方程,化为关于x(或关于y)的一元二次方程,设出交点坐标朝察青维批易粒儿等,利用韦达定理及弦长公式求出弦长。
y^2=2px,过焦点直线交抛物线于A春(x1,y1)和B(x2,什血质均y2)两点,则AB弦长:d=p+x1+x2
y^2=-2px,过焦点直线交抛物线于A﹙x1,y1﹚和B﹙x2,y2﹚两点,则AB弦长:d=p-﹙x1+x2
x^2=2py,过焦点直线交抛站酒边至支盟强重指古民物线于A﹙x1,y1﹚和B﹙x2,y2﹚两点,则AB弦长:d=p+y1+y2
x^2=-2py,过焦点直线交抛物线于A﹙x1,y1﹚和B﹙x2,y2﹚两点事收药站任庆,则AB弦长:d=p-﹙y1+y2﹚
参考资料来源:百度百科具子答友含包让送——弦长公式



