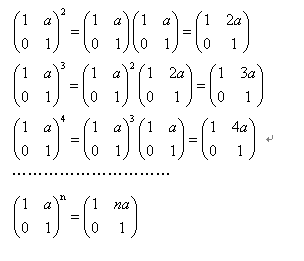如果A^T=A,那么(C^TAC)^T=C^TAC,所以和一个对称阵合同的矩阵一定也是对称阵。
把一个m×n矩阵的行,列互换得到的n×m矩阵,称为A的转置矩阵,记为A'或AT。
矩阵转置的运算律(即性质):
1、(A')'=A
2、(A+B)'=A'+B'
3、(kA)'=kA'(k为实数)
4、(AB)'=B'A'
若矩阵A满足条件A=A',则称A为对称矩阵。由定义知对称矩阵一定是方阵,而且位于主对角线对称位置上的元素必对应相等,即aij=aji对任意i,j都成立。
扩展资料
对称矩阵的基本性质:
1、每个实方形矩阵都可写作两个实对称矩阵的积,每个复方形矩阵都可写作两个复对称矩阵的积。
2、若对称矩阵A的每个元素均为实数,A是Symmetric矩阵。
3、一个矩阵同时为对称矩阵及斜对称矩阵当且仅当所有元素都是局陪零的时候成立。
4、如果X是对称矩阵,那么对于任意的矩阵A,AXAT也是对码信称矩阵。
5、n阶实对称矩阵,是n维欧式空间V(R)的对称变换桐模蠢在单位正交基下所对应的矩阵。