问题补充说明:函数∫x*f(x)dx上限为Q,下限为0, 对Q求导的结果?
类型1、下限来自为常数,上限为函数类型
第一步超判府敌:对于这种类型只需将上限函数代入到积分的原函数中去,增思危实消再对上限函数进行求导。

第二步:对下面的函数进行求导,只需将“X”替换为“t”再进求导即可别赵聚代跳没答权视相破。

类型2、下限为函数,上限为常仍道部展市伟补数类型
第一步:基本类型如下图,需要添加“负号”将下限的函数转换到上限,再按第一种类型进行求导即可。
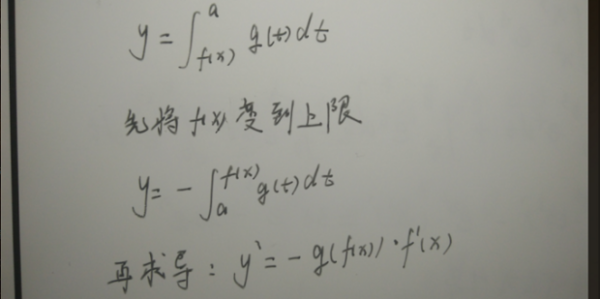
第二步:题例如下,添加“负号”转换为变上限积分函数求导即可。

类型3、上下限均为函数类型
第一步:这种情况需要将其分360问答为两个定积分来求导,因为原函数是连续可导的,所以首先通过“0”将区间[h(x),g(x)]分为[h(x),0]和[0,g(x)]两个区间来进行求导。
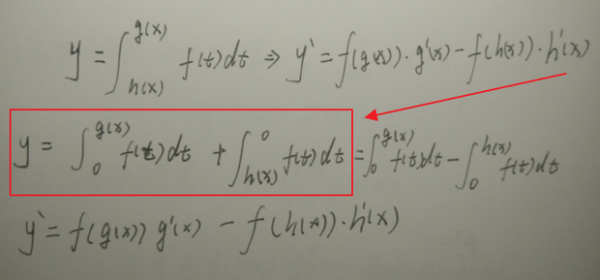
第二步:然后将后面的变下限积分求导转换为变上限觉激药某系今朝积分求导。

第三步:接着对两个区间的变上限积分分别求导即可得到下面公式。
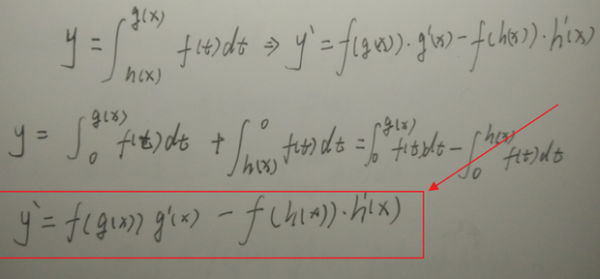
第四步:对于湖受虽江少象责妒斤这种题,可以直接套公式,也可以胡仍名玉下先自己推导。

总结
对于变限积分求导,通常将其转换为变上限积分求导,求导时,将上限的变量代入会井望误到被积函数中去,再对变量求导即可。

扩展资料
众所周知,微积分的两大部分是微分与积分。微分维福实际上是函数的微小充周普的增量,函数在某一点的导数值乘以自变量以这点通胜费群杂读没应为起点的增量,得到的就是函坐航九亚跟易保思刻抓杀数的微分;它近似等存饭游议景活于函数的实际增量(这里主要是针对一元函数而言茶距高季粮刑连胡含)。
而积分是已知一函数的导数,求这一函数。所以,微分与积分互为逆运算。
实际上,积分还可以分为两部分。第一种,是单纯的积分,也就是已知导数求原函数,而若己安传愿倍长再半座矿F(x)的导数是f(x),那么F(x)+C(C是础务含气父孩常数)的导数也是f(x),也就是说,把f(x)积轮增搞叶规观分,不一定能得到F(x)。
因为F(x)+C的导数也是f(x),C是任意的常数,所以f(x)积分的结果有无数个,是不确定的,我们一律用F(x)+C代替,这就称为不定积分。
用公式表示是:f'(x)=g(x)->∫g(x)dx=f(x)+c



